Diffie Hellman Calculator - fasrlosangeles. Diffie Hellman Calculator Mod N Receiver Sender calculate its public key as- Y s a X s mod n Receiver calculate its public key as- Y r a X r mod n Step-03. The Diffie-Hellman method works best if p = 2q+1 where q is also a prime. (For example, 5 and 11 are prime and 11 = 2 x 5 + 1.) Then half the integers 1,2.,p-1 are generators, and it is possible to check whether g is a.
You already use modulo computation when you look at the clock and e.g. needs to figure out what time it's 3 hours after 11 o'clock, which is 2 o'clock. In math we write that as:
( (11 + 3) : mod : 12 = 2 )
where 12 is the modulus because we want the time as an integer between 0 and 11 (12 o'clock is in this case denoted by 0). In words we say 11 plus 3 modulo 12 is equal 2. The result of a modulo computation is an integer between 0 and the modulus minus 1. E.g. with the modulus 3 we have that:
- ( 1 : mod : 3 = 1 )
- ( 2 : mod : 3 = 2 )
- ( 3 : mod : 3 = 0 )
- ( 4 : mod : 3 = 1 )
- ( 5 : mod : 3 = 2 )
- ( 6 : mod : 3 = 0 )
- etc.
If we e.g. look at ( 27 : mod : 5 ) then modulo computes the number of times 5 divides 27 and then returns the remainder of the result which is 2 in this case, i.e. ( 27 : mod : 5 = 2 ). But how did we get this result?
First we compute the number of times it's possible to multiply 5 with the number ( x ) such that we get an integer as close as possible to 27 without exceeding it, i.e. we have to find the maximun value of ( x ) such that ( 5 cdot x leq 27 ). In this case we have that ( x = 5 ) because ( 5 cdot 5 = 25 leq 27 ). Then by subtracting 27 with 25 we get the answer ( 27 - 25 = 2).
If the integer is negative e.g. ( -27 : mod : 5 ) we have to do it slightly different and the answer is ( -27 : mod : 5 = 3 ). In this case the integer ( x ) is negative and should be the closest integer that exceed -27, i.e. we have to find the minimum value of ( -x ) such that ( 5 cdot -x geq -27 ). Now we have that ( -x = -6 ) because ( 5 cdot -6 = -30 geq -27 ). Then by subtracting -27 with -30 we get the answer ( -27 - (-30) = -27 + 30 = 3).
It's important that ( x ) or ( -x ) is an integer such as ( -14, 3, 17 ) etc. and NOT a fraction or float such as ( frac{1}{4}, frac{-3}{7}, 2.5, 5.1 ) etc.
If two integers ( a ) and ( b ) modulo the same modulus ( c ) returns the same remainder ( r ), then we say that ( a ) and ( b ) are congruent modulo ( c ). I.e. if ( a : mod : c = r ) and ( b : mod : c = r ) then ( a equiv b : (mod : c) ). Also, notice that if the modulus ( c ) is greater than the integer ( a ), i.e. ( c > a ), the result will always be equal ( a : mod : c = a ).
Next: About this document Up:No Title Previous:No Title
Up:No Title Previous:No TitleA. The idea
Suppose two people, Alice and Bob [traditional names], want to use insecureemail to agree on a secret 'shared key' that they can use to dofurther encryption for a long message. How is that possible?The so-called Diffie-Hellman method provides a way. This methodis one of the ingredients of SSL, the encryption package that ispart of the Netscape browser.
These notes are a little more detailed than in class, for clarity,but on the exam you are responsible only for doing exercises like Problem 8.2.
B. The mod function
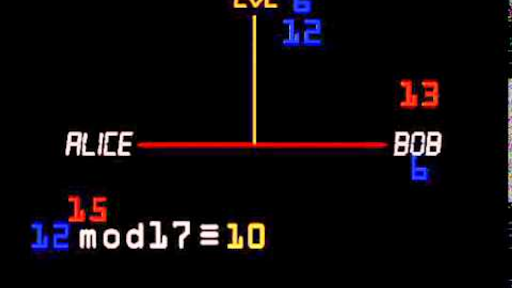
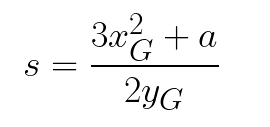
The main ingredient is the 'remainder' or 'modulo' or 'mod' function,denoted % in Perl. For example, 25%10 is 5 (say '25 mod 10is 5') and 25%16 is 9 ('25 mod 16 is 9'). For n%10,the result will always be one of 0,1,...,9.
As you can see, any positive integer modulo 10 is just the lastdigit in base 10: 1537%10 is 7, etc. You can think of'modulo 10' for positive integers as meaning 'ignore all decimaldigits except the last one'.
Doing 'modular arithmetic' with 'modulus' 10 means doingaddition, subtraction, and multiplication (including powers)where you only care about the remainder modulo 10. You can usesome other modulus m instead of 10, as long as it's the samethrough the whole problem. It works very smoothly.
The 'as often as you want' principle: If you are doingmodular arithmetic to find an the answer modulo m, you cantake the remainder modulo m as often as you want during thecalculations, without changing the answer.
Example 1. To find 1537 x 4248 modulo 10, you couldmultiply out and take the last digit, but a better way would beto replace 1537 by 7 and 4248 by 8 to start, find 7 x 8 =56, and then take 56 mod 10 to get 6 as the answer.
Diffie-hellman Calculator
A handy standard notation is to write a b (mod m) ifa and b have the same remainder modulo m. This is read'a is congruent to b modulo m'. In this notation theexample just mentioned looks like this: 1537 x 4248 7 x 8 = 56 6 (mod 10).
Example 2. Find 28 (mod 11).
One solution. 28 = 256; 11 goes into 256 with quotient 23and remainder 3.
Another solution. Find 22, 24, 28 by squaring repeatedly,but take remainders mod 11 each chance you get: 22 = 4,24 = 42 = 16 5, 28 52 = 25 3.
Example 3. Find all the powers of 2 up to 210 , each modulo 11.
Solution. Keep doubling, taking remainders modulo 11 wheneverpossible:
2, 4, 8, 16 5, 10, 20 9, 18 7, 14 3, 6, 12 1 (mod 11). So the answer is 2, 4, 8, 5, 10,9, 7, 3, 6, 1.
Notice that the powers of 2 run through all possible remaindersmodulo 11, except 0. We say 2 is a 'generator' modulo 11.There is a theorem that if you take a prime modulus, then thereis always some generator, and in fact 2 often works. If 2 doesn't,maybe 3 will.
C. The Diffie-Hellman method
The idea of Diffie and Hellman is that it's easy to computepowers modulo a prime but hard to reverse the process: Ifsomeone asks which power of 2 modulo 11 is 7, you'd have toexperiment a bit to answer, even though 11 is a small prime. Ifyou use a huge prime istead, then this becomes a very difficultproblem even on a computer. Steps:
- Alice and Bob, using insecure communication, agree on ahuge prime p and a generator g. They don't care if someonelistens in.
- Alice chooses some large random integer xA < p andkeeps it secret. Likewise Bob chooses xB < p and keeps itsecret. These are their 'private keys'.
- Alice computes her 'public key' yA gxA(mod p)and sends it to Bob using insecure communication. Bobcomputes his public key yB gxBand sends it toAlice. Here 0 < yA < p, 0 < yB < p.
As already mentioned, sending these public keys with insecurecommunication is safe because it would be too hard for someoneto compute xA from yA or xB from yB, just like thepowers of 2 above.
- Alice computes zA yBxA(mod p) and Bob computes zB yAxB(mod p). Here zA < p, zB < p.
But zA = zB, since zA yBxA (gxB)xA= g(xA xB) (mod p) and similarly zB (gxA)xB= g(xA xB) (mod p). Sothis value is their shared secret key. They can use it toencrypt and decrypt the rest of their communication by somefaster method.
In this calculation, notice that the step yBxA (gxB)xAinvolved replacing gxBby its remainder yB, (in the reversedirection) so we were really using the 'as often as you want'principle.

D. Notes (not on final exam)
Diffie Hellman Calculate
- It's easy to see why the 'as often as you want' principle works formodular arithmetic with positive integers in base 10. In Example 1,imagine doing the multiplication with paper-and-pencil arithmetic, butignoring everything except the last digit. You getIn other words, you can multiply and then take the last digit,or you can take remainders early, by saving just the 7 and 8,taking their product, and saving its last digit.
- Congruences work fine for negative numbers if you alwaysuse a remainder that is positive or 0; for example, -13 7 (mod 10)because -20 is a multiple of 10 and -13 is 7 larger. The
%operation in Perl works this way but the same operation inC and C++ does not. - The notation is meant to suggest =, becauseseveral properties of are similar to those of =.For example, a b and b c give a c (all mod m).
- Another interesting fact is that modulo 11, we have210 1, 310 1, 410 1,...,1010 1, and of course 110 =1 to startwith. More generally, there is a theorem saying that for anyprime p and for any a from 1 to p-1 we get ap-1 1(mod p).
- The Diffie-Hellman method works best ifp = 2q+1 where q is also a prime. (For example, 5 and 11 are prime and11 = 2 x 5 + 1.) Then half the integers 1,2,...,p-1 aregenerators, and it is possible to check whether g is agenerator just by seeing whether gq -1 (mod p).
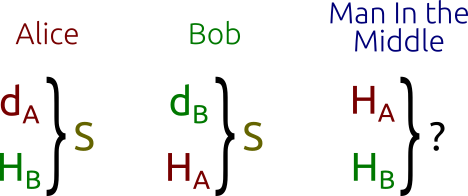
- Diffie-Hellman does have a weakness: If an intruderCharlie can intercept and resend email between Alice and Bob,then the intruder can pretend to be Bob for Alice and pretend tobe Alice for Bob, substituting his own yC and tricking eachof Alice and Bob into having a shared secret key with him.There are ways to fix this problem.
- The Diffie-Hellman method illustrates the concept of'public-key cryptography', where people can give out publicinformation that enables other people to send them encryptedinformation.
E. An example
For Diffie-Hellman to be secure, it is desirable to use a primep with 1024 bits; in base 10 that would be about 308 digits.An example, expressed in hexadecimal, is
p=de9b707d 4c5a4633 c0290c95 ff30a605 aeb7ae86 4ff48370 f13cf01c 49adb9f23d19a439 f743ee77 03cf342d 87f43110 5c843c78 ca4df639 931f3458 fae8a94d1687e99a 76ed99d0 ba87189f 42fd31ad 8262c54a 8cf5914a e6c28c54 0d714a5f6087a172 fb74f481 4c6f968d 72386ef3 45a05180 c3b3c7dd d5ef6fe7 6b0531c3
z=56c03667 f3b50335 ad532d0a dcaa2897 a02c0878 099d8e3a ab9d80b2 b5c83e2f14c78cee 664bce7d 209e0fd8 b73f7f68 22fcdf6f fade5af2 ddbb38ff 3d2270cebbed172d 7c399f47 ee9f1067 f1b85ccb ec8f43b7 21b4f980 2f3ea51a 8acd1f6fb526ecf4 a45ad62b 0ac17551 727b6a7c 7aadb936 2394b410 611a21a7 711dcde2
To compute with huge integers like these, you need a special 'multipleprecision' software package, because the built-in arithmeticon computer chips handles only 32 or 64 bits.
F. Solution to the homework problem
Here p=11, g=2, xA = 9, xB = 4. So yA = 2xA= 29 (mod 11).
You can find this most easily by finding 22 =4, 24 = 42 = 16 (mod 11), 28 = (24 )2 52 = 25 3 (mod 11), andfinally 29 = 2 x 28 2 x 3 = 6. So yA = 6.
Similary, 2xB= 24 = 16 5 (mod 11), so yB = 5.
The secret shared key zA is the remainder of yBxA= 59 (mod 11). So find 52 = 25 3 (mod 11), 54 =(52 )2 32 = 9 (mod 11), 58 = (54 )2 92 = 81 4 (mod 11), 59 = 5 x 58 5 x 4 = 20 9(mod 11). As a check, zB is the remainder of yAxB= 64 (mod 11). 62 = 36 3 (mod 11) so 64 = (62 )2 32 = 9 (mod 11), which checks. So zA = zB = 9.
Next: About this document Up:No Title Previous:No TitleKirby A. Baker
Sun Mar 21 19:36:51 PST 1999